Im der Übung werden die Methoden der aus dem Unterricht gewohnten Elementargeometrie
unverfroren auf eine Karte der Zeichenebene angewendet und dabei wie nebenbei
gelernt, wie Hypothesen gefunden werden, aus denen sich eine Theorie entwickeln kann.
Die benutzten json-Programme arbeiten unter einem Zeichenprogramm ,
das speziell von Stefan Liebscher
für die projektive Geometrie entwickelt wurde.
Mit dem button "Import" können die json-Dateien aufgerufen werden. |
|
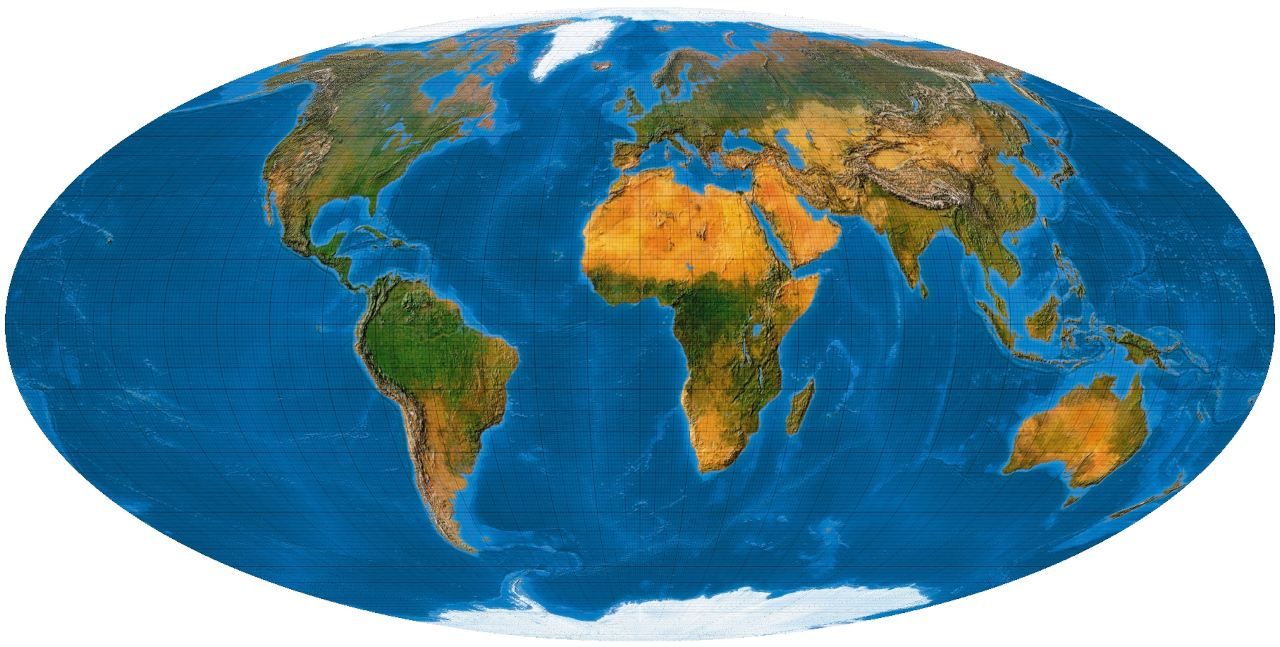
Weltkarten kennen wir alle. Sie sollen den Rand des Zeichenblatts nicht überschreiten
und die Lage der Orte zueinander wenigstens andeutungsweise wiedergeben. Man nennt die verschiedenen Darstellungen
Projektionen, obwohl genau genommen nicht projiziert, sondern nur verzerrt wird:
Der Maßstab ist an jeden Punkt ein anderer. Was auf der Kugel Geraden (Großkreise) sind,
wird zu schwierigen Kurven, und es ist ohne weiteres nicht zu sehen, wie man nun noch
geometrisch konstruieren kann.
|
|
|
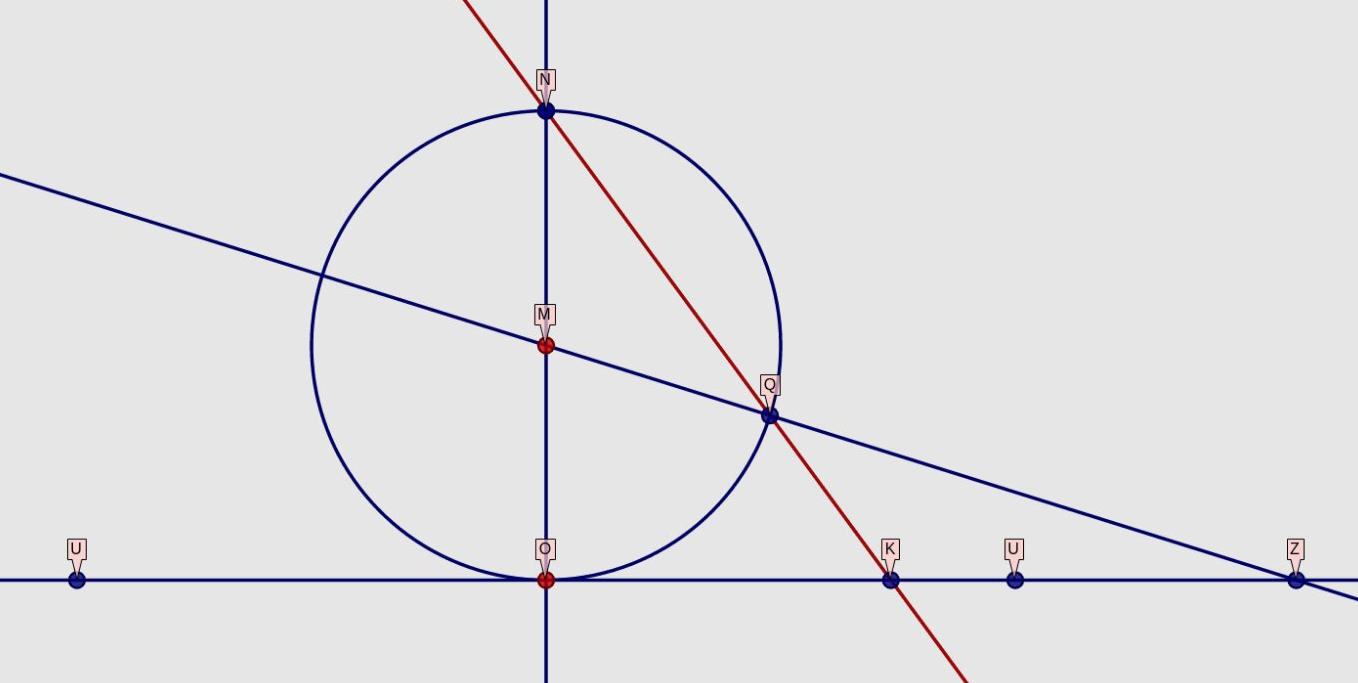
Ein einfaches, aber weitreichendes Beispiel ist eine Karte der Zeichenebene selbst. Parallelen
treffen sich im Unendlichen, sagt man ganz locker. Gerade um das zu sehen, brauchen wir eine geeignete Karte der Zeichenebene,
das heißt ein Bild, in dem das Unendliche selbst abgebildet ist. Wir wählen eine Karte, auf welcher der Abstand R von einem Punkt O der Zeichenebene
auf einen kleineren
Abstand r für die Karte umgerechnet wird, wobei r[R] eine monotone Funktion, die auch für beliebig große
Werte von R kleiner als ein fester Wert D bleibt und finden einen Kreis, dessen Inneres jetzt die gesamte Zeichenebene abbildet.
Setzen wir vielleicht eine Kugel mir Durchmesser D auf die Zeichenebene, kann diese aus dem Mittelpunkt auf die untere Halbkugel projziert
werden. Wenn wir dann diese untere Halbkugel aus dem Nordpol auf die Ebene zurückprojizieren, erhalten wir einen Kreis,
die die gesamte unendliche Zeichenebene kartiert.
|
|
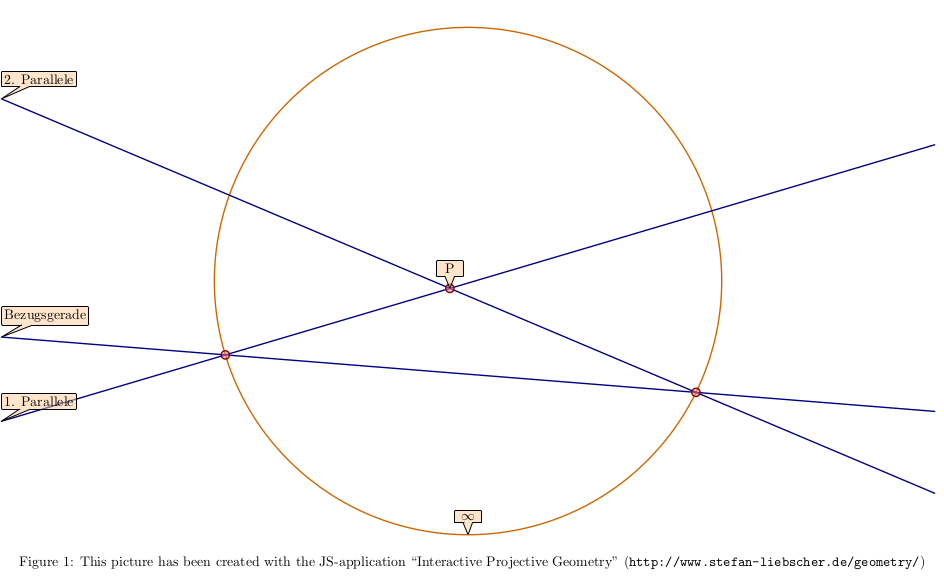
Die Geraden und Kreise der Zeichenebene sind auf der Karte nicht mehr gerade oder kreisrund.
Im eben gezeigten Beispiel der Erzeugnung der Karte durch eine Mittelpunkts- und eine
stereographische Projektion sind sie immerhin noch Kegelschnitte, aber auch in diesem Spezialfall kommt
man nicht elementar weiter. Kann man mit Zirkel und Lineal noch etwas anfangen?
Versuchen wir es mit dem Lineal, d.h. mit den Geraden auf der Karte, und übernehmen, was von den
Geraden der abgebildeten Zeichenebene bekannt ist:
Geraden sind unbegrenzte Kurven, die sich höchstens einmal schneiden.
Geraden sind Spiegel, die Geraden in Geraden spiegeln, Schnittpunkte in Schnittpunkte,
und welche die Punkte auf dem Spiegel unverändert lassen.
Es gibt nun Geraden, die sich noch nicht einmal im Unendlichen (d.h. auf dem Kreis U) schneiden,
und durch einen Punkt P neben einer Geraden g gibt es zwei Geraden, die g im Unendlichen schneiden,
sozusagen 2 Parallelen. Wir befinden uns in einem Modell der nichteuklidischen Geometrie, deren Existenz
allein ein berühmtes Rätsel war.
Ohne jetzt darüber tiefer nachzudenken,
kommen wir zum entscheidenden Punkt. Kein gewöhnlicher Punkt wird ins Unendliche gespiegelt.
Punkte im Unendlichen werden wieder auf Punkte im Unendlichen gespiegelt. Das ist alles was wir brauchen. Na, dann man los.
|
|
|
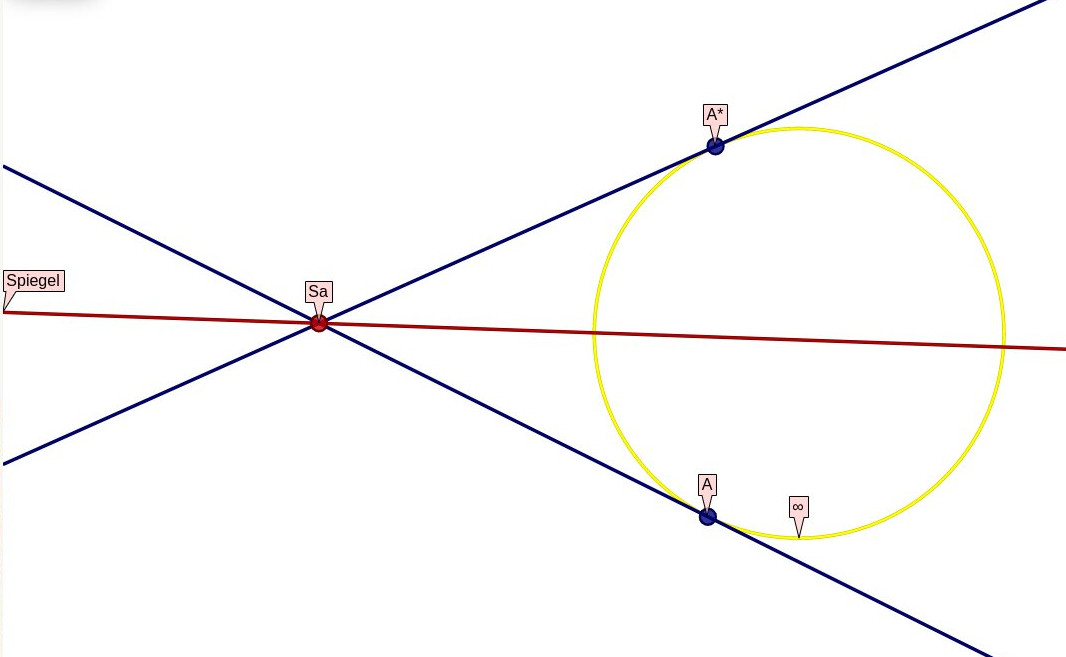
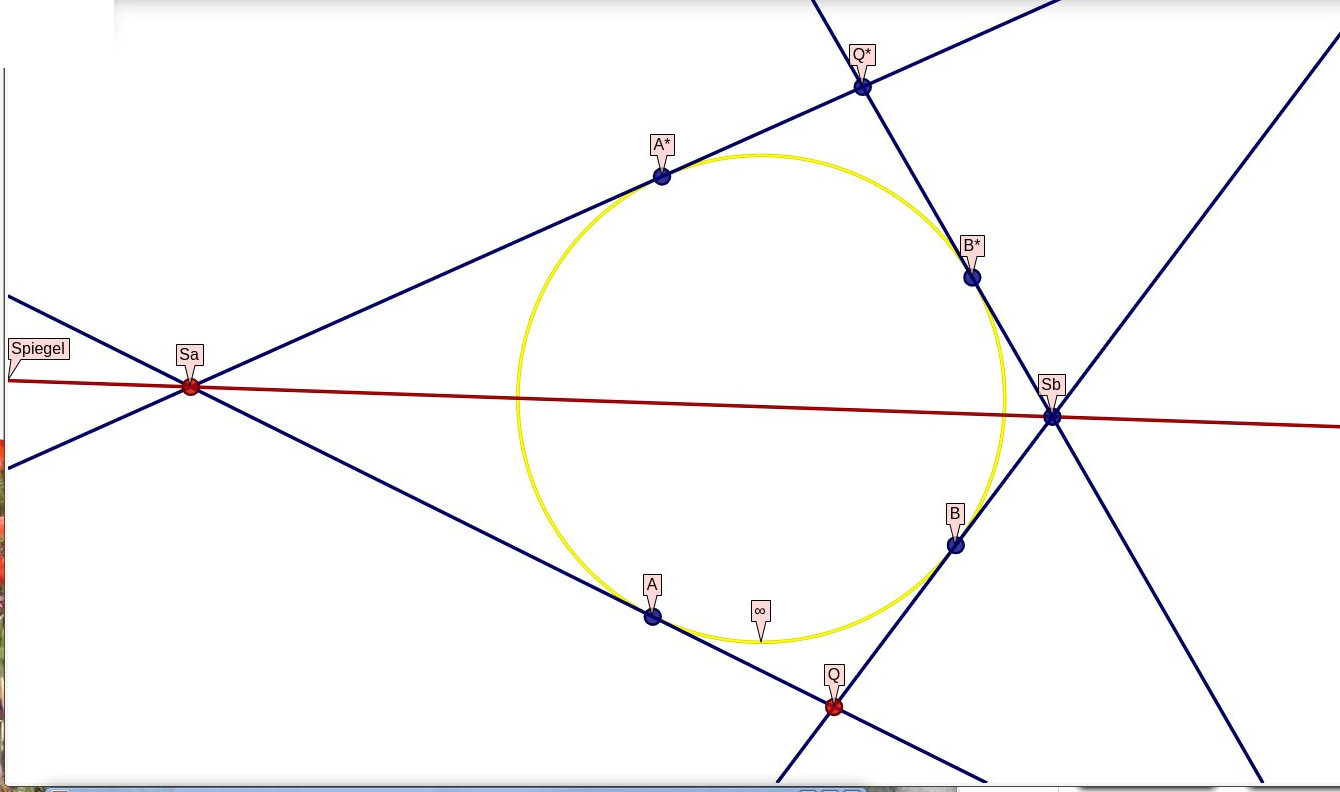
Das Unendliche ist auf unserer Karte jetzt ein Kreis. Wir ziehen eine Gerade, die wir als
Spiegel s benutzen wollen und betrachten zuerst das Spiegelbild des Unendlichen U.
Der Kreis kann sich nicht verändern, das Unendliches soll ja unendlich bleiben. Folglich muss das Spiegelbild eines Punktes A
auf U auch wieder auf U liegen, das Spiegelbild einer Tangente an U
muss wieder eine Tangente sein.
Schneidet die Tangente an A den Spiegel in Sa, so ist ihr Bild die andere Tangente aus Sa
an den Kreis U,
der das Unendliche kartiert.
|
|
Von einem Punkt Q außerhalb des Unendlichen U können wir zwei Tangenten ziehen, die den Spiegel in Sa und Sb
schneiden. Die Spiegelbilder dieser Tangenten sind die jeweils anderen Tangenten durch diese Punkte. Ihr Schnittpunkt Q* ist also
das Spiegelbild von Q.
Das Spiegelbild einer Geraden, die das Unendliche in A und B schneidet, finden wir als Verbindung deren Spiegelbilder A* und B*.
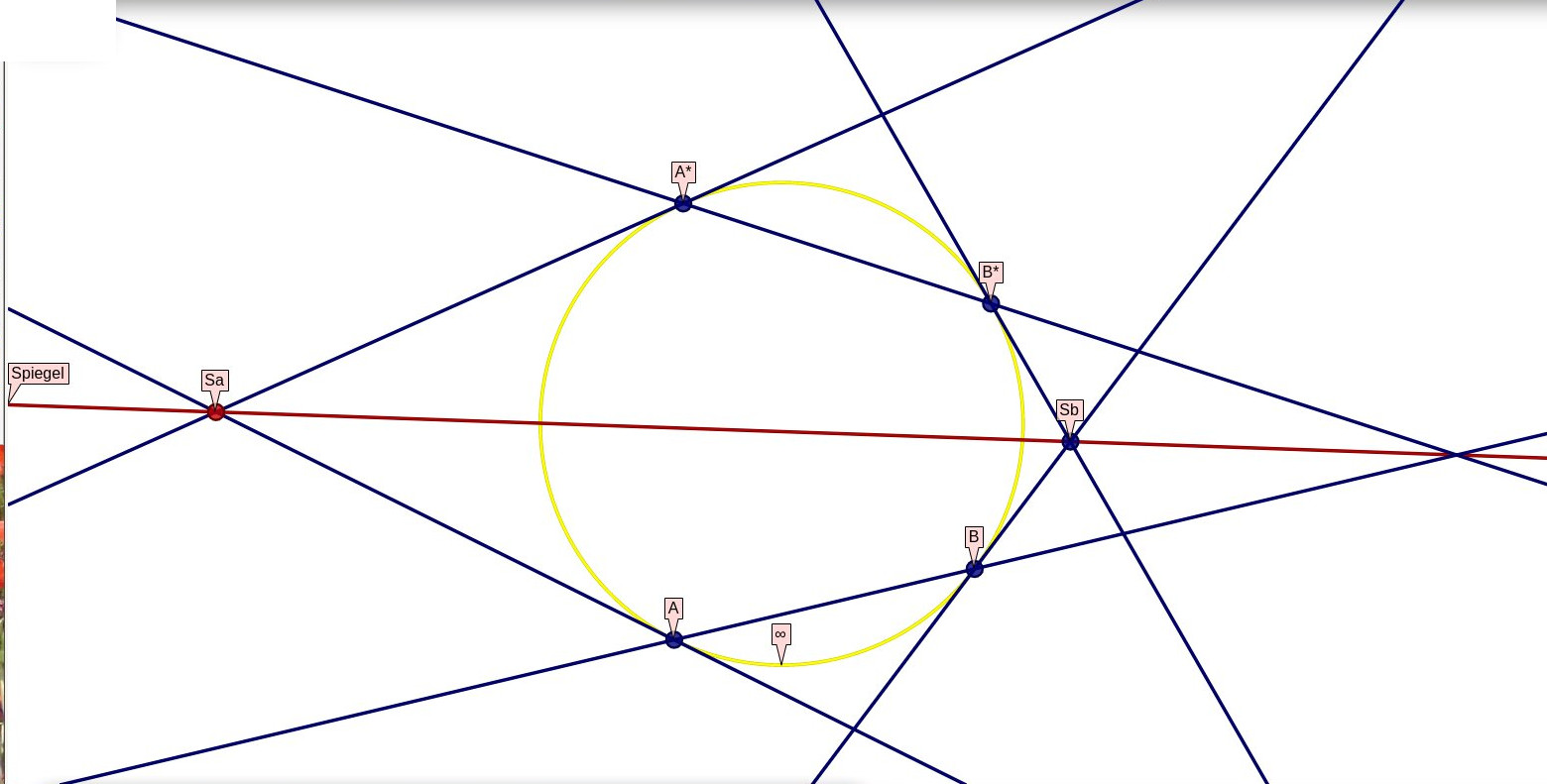
Suchen wir das Spiegelbild eines Punktes im Endlichen (d.h. innerhalb U), sehen wir ihn als Schnittpunkt zweier Geraden, deren eben konstruierte
Spiegelbilder sind dann im Spiegelbild des Punktes schneiden. Suchen wir das Spiegelbild einer Geraden, die U nicht schneidet, wählen wir zwei Punkte auf ihr
und finden das Spiegelbild der Geraden als Verbindung der Spiegelbilder dieser Punkte.
|
|
Alle Kongruenz wird nun mit solchen Spiegelungen prüfbar, und man findet viele Ähnlichkeiten mit der Geometrie auf dem ursprünglichen Zeichenblatt.
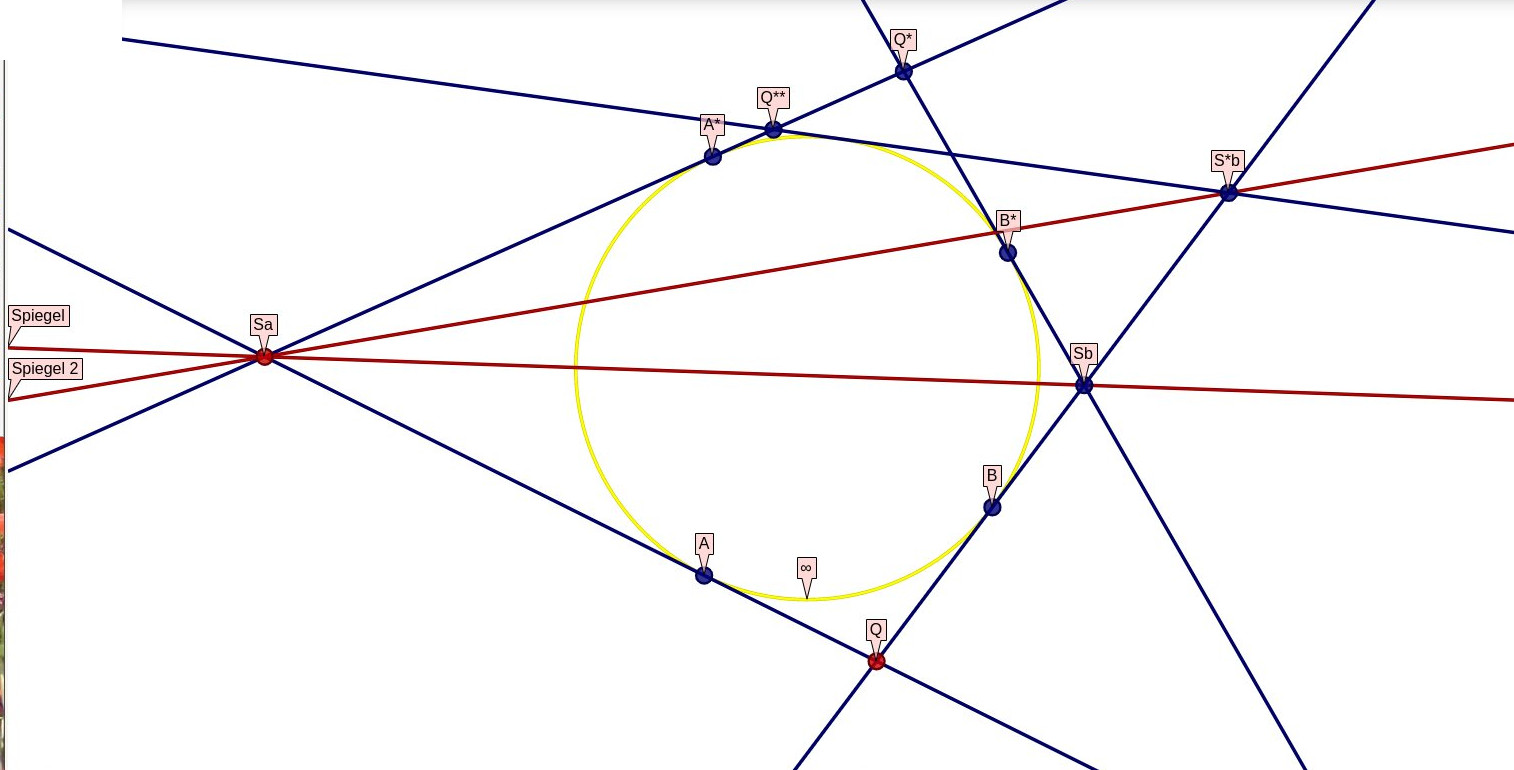
Das lassen wir aber, und konstruieren lieber den verblüffenden Beweis, dass Umwege jenseits des Unendlichen (d.h. außerhalb des Kreises U)
kürzer sind als die direkten:
Legen wir durch Sa einen zweiten Spiegel, finden wir das zu diesem gehörende Bild von Q in Q**.
Dieser Punkt liegt auf der gleichen Tangente wie das erste Bild Q*. Nun ist SaQ* kongruent SaQ, und dieses wiederum
kongruent zu SaQ**. Wenn zwei verschiedene zueinander proportionale Strecken das gleiche Maß haben, muß das Maß null sein.
Eine Strecke auf einer Tangente an U hat die Länge Null.
Wie groß das Maß - die Länge - einer Strecke S*bQ* auch ist, der Umweg über die beiden Tangenten hat die Gesamtlänge Null.
Diese Verhältnisse finden sich in der Relativitätstheorie als Zwillingsparadoxon wieder, aber das ist ein anderes Thema.
|
|
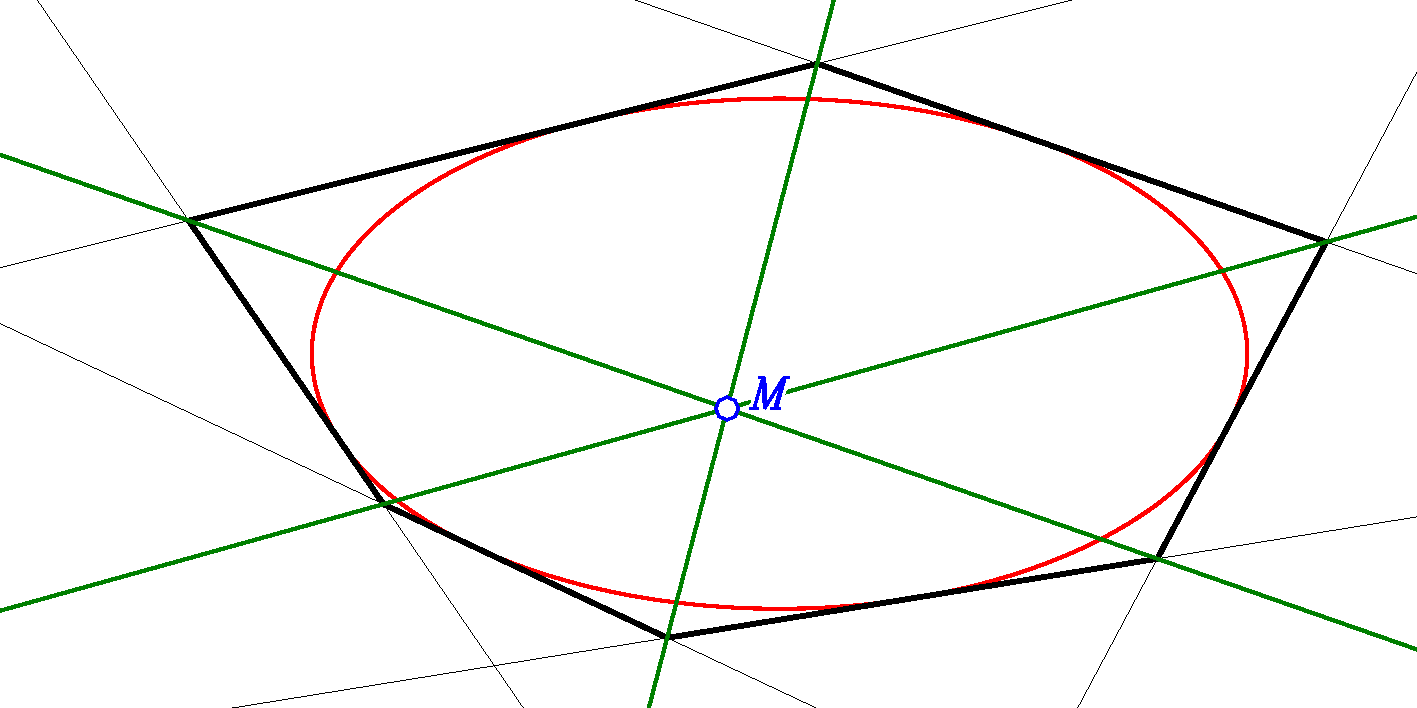
Wenn Spiegelungen das Mittel zum Längenvergleich sein sollen,
müssen sich die Mittelsenkrechten
eines Dreiecks in einem Punkt schneiden.
Die Spiegel für die drei Punktepaare eines Dreiecks bilden ein Tangenten-Sechsseit an Kreis ∞.
Der Satz des Brianchon (der u.a. die Kegelschnitte definiert) muss hier immer greifen, deshalb muss die Kurve,
die das Unendliche abbildet, immer ein Kegelschnitt sein
(json-Programm dazu).
Satz des Brianchon: Ein Sechsseit ist einem Kegelschnitt umschrieben, wenn die Verbindungen der Schnittpunkte
gegeüberliegender Seitenpaare sich in einem Punkt traffen.
Der Umkreismittelpunkt ist dann dieser Schnittpunkt (hier das Umkreismittenprogramm).
|
|
|
Unerwartet ist dass es zwie Symmetrieachsen zu einem Punktepaar gibt. Die zweite Symmetrieachse ist in der
euklidischen Geometrie immer unendlich fern, jetzt aber sichtbar
(json-Programm dazu).
Die Strecke AB hat jetzt zwei Seitenmitten, die die Strecke AB harmonisch teilen.
Ist die Punktreihe ACBD kongruent zu ADBC heißt die Teilung von AB durch CD
harmonisch. Das vollständige Vierseit ist die Schlüsselkonstruktion
(movie dazu).
|

|
|
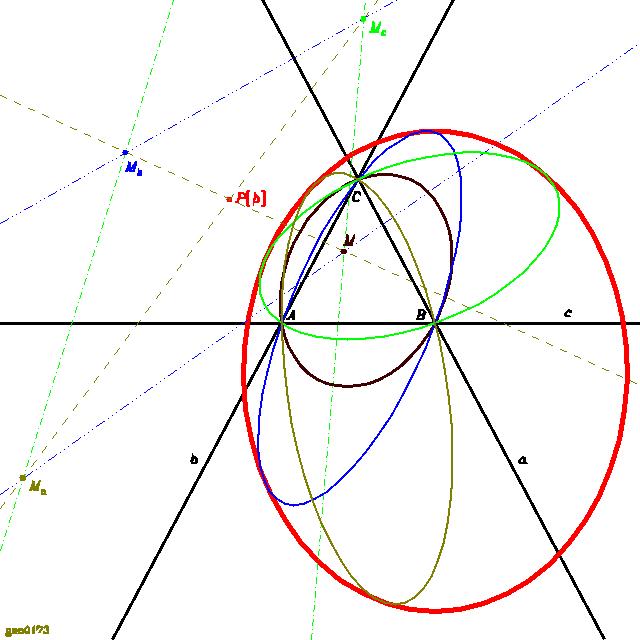
Weil nun jede Seite zwei Mitten und zwei
Mittelsenkrechten hat, gibt es vier Schnittpunkte und vier Umkreise des
Dreiecks. Die Umkreise berühren zwei Mal das Unendliche, nur einer von
ihnen eventuell nicht. Diesen sehen wir in der gewohnten euklidischen
Geometrie (json-Programm dazu).
Wenn von zwei Kegelschnitten einer zum Bild des Unendlichen deklariert
wird und der andere dann ein Kreis ist, wird der erste ein Kreis, wenn
der zweite die Darstellung des Unendlichen übernimmt. Man kann also
definieren: Zwei Kegelschnitte sind zueinander Kreis, wenn sie sich
zweimal berühren, die vier Schnittpunkte also zwei Doppelpunkte werden
(die auch alle komplex sein können).
|
|
|
Die gewohnte Dreiecksungleichung gilt nur im Innenraum des absoluten Kegelschnitts.
Im Außenraum kann sie nicht gelten, wie oben schon dargestellt ist.
Zwei der Seiten eines Dreiecks sollen auf die dritte gespiegelt werden.
Die Spiegel sind die Winkelhalbierenden.
Winkelhabierende zweier Geraden sind die Polaren der Mittelpunkte der beiden Pole.
Nach der Spiegelung der Punktes C an den beiden Spiegeln
(json-Programm dazu)
kann man das Stück, das AB länger als ACB ist, direkt sehen.
Satz und Zeichnung finden sich in der Relativitätstheorie als
Zwillingsparadoxon wieder.
|

|
|
Nur in der gewohnten euklidischen Geometrie hat ein Rechteck vier Seiten.
In der hier skizzierten nicht-euklidischen Geometrie haben Rechtecke
5 oder mehr Seiten. Hier ist ein
json-Programm für die Konstruktion eines
fünfseitigen Rechtecks und ein
json-Programm zur Darstellung
der Pole der fünf Seiten.
Wie in der euklidischen Ebene auch, kann man mit regulären Rechtecken (dort Quadrate)
die Ebene parkettieren. Mit Fünfecken geht das noch ganz übersichtlich.
Mauritz Escher hat ein Parkett mit rechteckigen Sechsecken gezeichnet, nur hat
er nicht die geradentreue, sondern die winkeltreue Karte (das Poincaré-Modell) der
nicht-euklidischen Geometrie benutzt, wo Kreisbögen die Rolle
der Geraden unserer Darstellung übernehmen.
|


|
nach 











