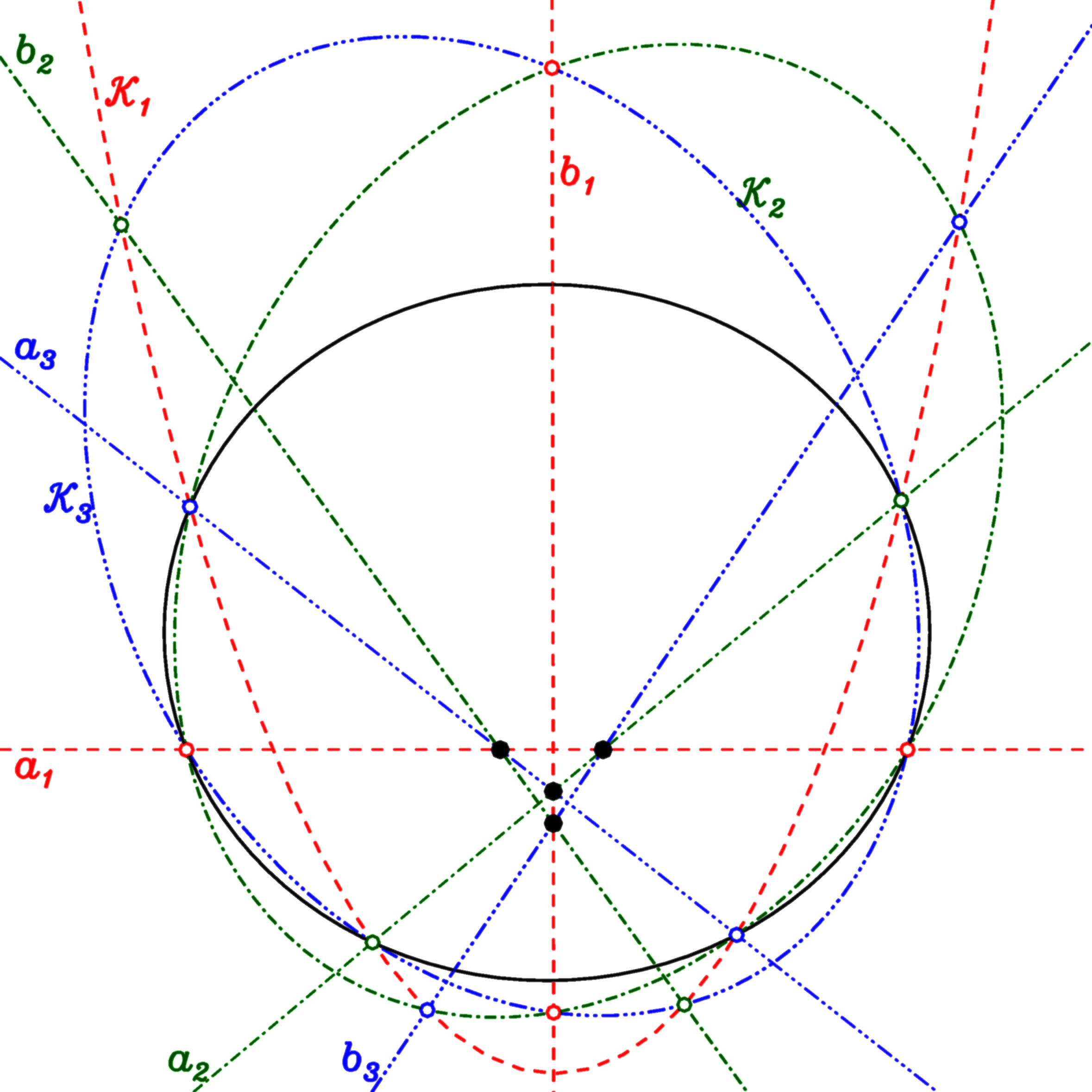
Three asymptote-sharing conics
define a quadrangle of intersections of common chords. Here, the black circle is the absolute conic, which serves the asymptotic points as intersections with the green, red and blue conics. In the case shown, all these intersections are real, and because of the required sharing, they are only six instead of twelve. The three conics intersect each other too, and produce further six points. The six connecting lines of opposite intersections form the edges of a quadrangle.| Kapitel Portal |
|